<股票配资网大全>高中数学：深入解析组合函数单调性与最值的应用要点

#组合函数的单调性与最值问题#关键词：高中数学、函数、单调性、增函数、减函数、应用

一、引言

函数的单调性是数学中的重要概念，也是高中数学的核心内容之一。它描述了函数值随自变量变化而变化的趋势，是分析和理解函数性质的基础。本文将深入解析函数的单调性，帮助读者更好地理解和掌握这一重要概念。

二、函数单调性的定义

函数的单调性是指函数在某个区间内，随着自变量的增加或减少，函数值也相应地增加或减少的性质。具体来说，如果对于任意两个自变量x1和x2（x1 < x2）高中数学：深入解析组合函数单调性与最值的应用要点，都有f(x1) ≤ f(x2)，则称函数在这个区间内是单调增加的；如果对于任意两个自变量x1和x2（x1 < x2），都有f(x1) ≥ f(x2)，则称函数在这个区间内是单调减少的。

三、判断函数单调性的方法

导数法：通过求导判断函数的单调性。如果函数在某个区间内的导数大于0，则函数在该区间内单调增加；如果导数小于0，则函数在该区间内单调减少。

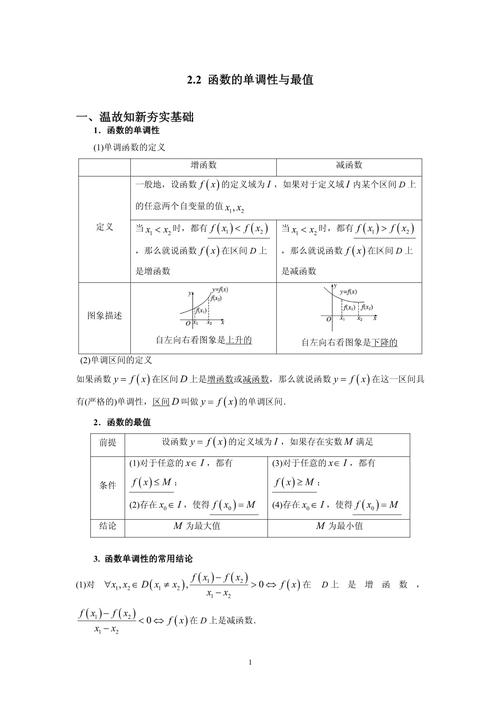
图像法：通过观察函数的图像来判断函数的单调性。如果函数的图像在某个区间内是上升的，则函数在该区间内单调增加；如果图像是下降的，则函数在该区间内单调减少。

差分法：通过比较函数值的变化来判断函数的单调性。如果对于任意两个相邻的自变量x1和x2（x1 < x2），都有f(x2) - f(x1) > 0，则函数在该区间内单调增加；如果f(x2) - f(x1) < 0，则函数在该区间内单调减少。

四、函数单调性的应用

函数的单调性在实际生活中有着广泛的应用。例如，在经济学中，我们可以用函数的单调性来分析市场供需关系的变化趋势；在物理学中，我们可以用函数的单调性来描述物体的运动状态；在工程技术中，我们可以用函数的单调性来优化设计方案等。因此，掌握函数的单调性对于我们理解这些实际问题有着重要的意义。

五、典型问题解析

通过举例分析一些典型问题，如判断函数的单调性、求函数的单调区间等，帮助读者更好地理解和掌握函数的单调性及其在实际问题中的应用。

六、总结与展望

本文通过对高中数学中函数的单调性进行深入解析，帮助读者更好地理解和掌握这一重要概念。通过学习和掌握函数的单调性及其判断方法，读者可以更加深入地理解数学中的基本概念和运算规则函数的单调性和最值，提高逻辑思维能力和数学素养。同时，我们也应该意识到函数的单调性在数学中的重要地位和作用，不断探索其在各个领域的应用前景和发展空间。